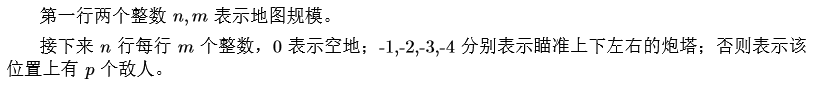[网络流]tower
tower
Time Limit: 10 Sec Memory Limit: 256 MB
Description
Nick近在玩一款很好玩的游戏,游戏规则是这样的:
有一个n*m的地图,地图上的每一个位置要么是空地,要么是炮塔,要么是一些BETA狗,Nick需要操纵炮塔攻击BETA狗们。
攻击方法是:对于每个炮塔,游戏系统已经给出它可以瞄准的方向(上下左右其中一个),Nick需要选择它的攻击位置,每一个炮塔只能够攻击一个位置,炮塔只能够向着它的瞄准方向上的某个位置发动攻击,当然炮塔也可以不进行攻击。炮塔威力强大,它可以且仅可以消灭目标位置上所有的BETA狗。出于安全考虑,游戏系统已经保证不存在一个炮塔能够瞄准另外一个炮塔,即对于任意一个炮塔,它所有可能的攻击位置上不存在另外一个炮塔。而且,如果把炮塔的起点和终点称为炮弹的运行轨迹,那么系统不允许两条轨迹相交f包括起点和终点)。现在,选定目标位置以后,每一个炮塔同时开炮,你要告诉Nick,他最多可以干掉多少BETA狗。
Input
Output
一行一个整数表示答案。
Sample Input
4 5
0 0 -2 0 0
-4 0 5 4 0
0 -4 3 0 6
9 0 0 -1 0
Sample Output
12
HINT
Main idea
给定若干固定方向的炮台,以及若干位置的敌人,炮台可以杀掉对应方向上从该位置到底的其中一个位置的敌人,要求炮台位置和消灭的敌人位置连线,连线不能有重叠,询问最多能消灭几个敌人。
Solution
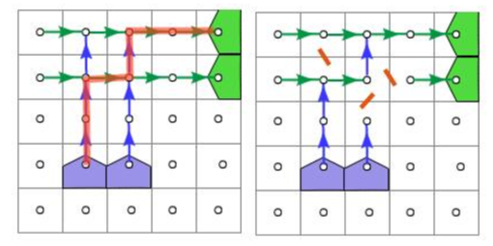
我们发现,相交的连线其实就是给出了炮台之间的路径。我们来处理如何解决无可走路径的问题,显然想到了最小割。
横向炮台或纵向炮台之间是没有影响的。所以显然可以构建一张二分图。
那么我们如何确定容量呢?我们可以令一条 (u->v) 的割边表示选择了u这个点。方便处理连边上下或左右攻击的炮台,连边方向应该一致。然后我们连边时先找到一条可攻击位置上的最大贡献,设最大贡献为Max,然后连边时容量用Max-val,就表示它会损失这么多的价值。注意到这样连边的话,在最边界上的点是没有连边的。但是并不会影响答案,为什么呢?我们这么考虑:如果我们选择了最边界的点,那么这个位置的敌人数必然是最多的,如果不是最多的话(也就是说还有其它点人数更多)显然连到边界不可能是最优的,因为连边界就可能阻断了更多其它炮台攻击方案的可能性。这就表示了,若选择边界,则必然边界贡献最多,那么如果连边了,容量也应该是0,综上所述不会影响答案。
我们这样连完了边,但发现还是会有一些问题。如果出现这种情况,就会有一些Bug:
这样就会影响了答案。怎么处理呢?我们发现问题只能涉及一行一列,只要令路径只能“拐一次弯”就可以解决。所以我们可以再将点拆为横向点和纵向点,横向点向纵向点连INF的边,纵向点没有边连向横向点即可。
这样的话复杂度就是O(maxflow(n×m,n×m)),成功了解决了问题!(≧▽≦)/
Code
1 |
|